Fluência Sem Medo: Pesquisas Mostram as Melhores Formas de Aprender Fatos Matemáticos
Jo Boaler, Professora de Educação Matemática e co-fundadora do youcubed
Com a colaboração de Cathy Williams, co-fundadora do youcubed, e Amanda Confer, da Universidade de Stanford
Introdução
Alguns anos atrás, o político britânico Stephen Byers cometeu um erro inofensivo durante uma entrevista. Pediu-se ao muito honorável ministro a resposta para (7 x 8) e ele respondeu “54”, em vez do que é o correto: “56”. Seu erro gerou uma ridicularização generalizada na mídia nacional, acompanhada de pedidos a favor da memorização das “tabuadas” nas escolas. Em setembro passado, o ministro da Educação do partido conservador da Inglaterra, um homem sem qualquer experiência nessa área, insistiu que, aos 9 anos de idade, todos os alunos ingleses deveriam ter decorado a tabuada até o (12 x 12). Essa exigência foi agora inserida no currículo de matemática do Reino Unido e vai resultar, creio, no aumento da ansiedade e da repulsa dos alunos em relação à matemática em números recorde. Os Estados Unidos estão indo na direção oposta, pois os Padrões Estaduais (Common Core State Standards – CCSS) tiram a ênfase de decorar fatos na matemática. Infelizmente, interpretações errôneas do significado da palavra “fluência” nos CCSS são recorrentes, e as editoras continuam a dar ênfase ao decorar, encorajando a manutenção de práticas de sala de aula danosas em todos os Estados Unidos.
Os fatos matemáticos são importantes, mas sua memorização por meio da repetição de tabuadas, prática e testes cronometrados é desnecessária e danosa. O erro do ministro inglês, quando questionado sobre o resultado de (7 x 8), gerou clamores por mais memorização. Isso é algo irônico, uma vez que o fato revelou, na verdade, as limitações da memorização sem o “senso numérico”. Pessoas com senso numérico são aquelas que conseguem usar números com flexibilidade. Quando solicitadas a resolver a multiplicação (7 x 8), elas podem ter o número 56 gravado na memória, mas também conseguiriam calcular que (7 x 7) dá 49, e então acrescentariam 7 para fazer 56, ou somariam dez 7’s e subtrairiam dois 7’s (70-14). Não dependeriam, portanto, de uma memória distante. Os fatos matemáticos, em si, compõem uma pequena parte da matemática e são mais bem absorvidos por meio do uso dos números em diferentes formas e situações. Infelizmente, muitas salas de aula focam em fatos matemáticos de formas improdutivas, dando aos alunos a impressão de que estes são a essência da matemática, e, ainda pior, de que o aluno que se sai bem na disciplina é aquele que tem as respostas na ponta da língua. Ambas as ideias estão erradas e é crucial que as removamos de sala de aula, pois elas exercem um importante papel na produção de ansiedade e no descontentamento dos alunos em relação à matemática.
É útil guardar algumas coisas na memória. Eu não paro e penso na resposta de (8 + 4), porque sei o fato matemático. Mas eu os aprendi usando-os em diferentes situações matemáticas e não os praticando e sendo testada. Cresci em uma época progressista da Inglaterra, quando as escolas primárias focavam na “criança como um todo”, e eu não recebia tabelas com fatos de adições, subtrações ou multiplicações, os quais precisaria memorizar. Isso nunca representou um empecilho em qualquer época ou lugar da minha vida, apesar de eu ser professora de educação matemática. E isso se dá porque eu tenho senso numérico, algo muito mais importante para o aprendizado dos alunos, pois inclui o aprendizado de fatos matemáticos atrelado a uma profunda compreensão dos números e das maneiras como eles se relacionam entre si.
Senso Numérico
Em um projeto de pesquisa crítico, pesquisadores analisaram alunos com idades entre 7 e 13 anos enquanto resolviam problemas numéricos (GRAY; TALL, 1994). Eles haviam sido identificados por seus professores por meio de sua taxa de desempenho: baixa, média e alta. Os alunos de alto desempenho usavam o senso numérico; os de baixo desempenho, não. Os alunos de alto desempenho abordavam um problema, por exemplo, (19 + 7), transformando-o em (20 + 6). Nenhum aluno identificado na categoria de baixo desempenho usava o senso numérico. Quando estes recebiam problemas de subtração, tais como (21 – 16), eles contavam de trás pra frente, começando com 21 e fazendo uma contagem decrescente, o que é extremamente difícil. Os alunos de alto desempenho, por sua vez, usavam estratégias tais como transformar os números em (20 – 15), algo muito mais fácil de fazer. Os pesquisadores concluíram que os alunos, geralmente, apresentam baixo desempenho não porque sabem menos, mas porque não usam os números de forma flexível; ou seja, seguem o caminho errado, geralmente desde pequenos, tentando memorizar métodos em vez de interagir com os números de forma flexível (BOALER, 2009). Esse caminho incorreto significa que eles, via de regra, estão aprendendo uma matemática mais difícil e, lamentavelmente, acabam enfrentando uma vida inteira de problemas com a disciplina.
O senso numérico é a base da matemática de alto nível (FEIKES; SCHWINGENDORF, 2008). Quando os alunos não passam em álgebra, isso geralmente está vinculado à falta de senso numérico. Quando executam problemas matemáticos ricos – tais como os que oferecemos ao final deste artigo – desenvolvem senso numérico e também aprendem e memorizam os fatos matemáticos. Ao focarem na memorização de tabuadas, os alunos geralmente memorizam fatos sem senso numérico, o que significa que suas ações são muito limitadas e estão propensas a ser equivocadas – tais como a que levou o político britânico a ser ridicularizado nacionalmente. A falta do senso numérico tem causado erros catastróficos: um exemplo é o que ocorreu com o telescópio Hubble, ao não encontrar as estrelas que deveria fotografar no espaço. O telescópio estava procurando as estrelas em uma certa constelação, mas falhou devido ao erro aritmético de alguém que estava encarregado de sua programação (LA TIMES, 1990). O senso numérico, criticamente importante para o desenvolvimento matemático dos alunos, é inibido pelo excesso de ênfase na memorização de fatos matemáticos em sala de aula e em casa. Quanto mais se enfatiza a memorização dos alunos, menos eles estarão dispostos a pensar sobre os números e suas relações, bem como usar e desenvolver o senso numérico (BOALER, 2009).
O cérebro e o senso numérico
Alguns alunos não têm tanta habilidade para memorizar fatos matemáticos quanto outros. Isso é algo a ser celebrado, pois faz parte da maravilhosa diversidade da vida e das pessoas. Imagine o quanto seria chato e pouco inspirador se os professores dessem testes de matemática e os alunos os respondessem da mesma forma e com a mesma velocidade, como se fossem robôs. Em um estudo recente, os cientistas examinaram o cérebro dos estudantes enquanto eles eram ensinados a memorizar fatos matemáticos, e perceberam que alguns alunos os memorizavam com muito mais facilidade do que outros. Isso não será surpresa alguma para os leitores e muitos de nós, provavelmente porque presumiríamos que aqueles que memorizavam melhor eram os alunos de alto desempenho ou os “mais inteligentes”. Contudo, os pesquisadores descobriram que os alunos que memorizavam com mais facilidade não eram os de alto desempenho, pois não tinham o que eles descreveram como maior “habilidade matemática”, tampouco tinham QI’s mais altos (SUPEKAR et al, 2013). As únicas diferenças que os pesquisadores descobriram estavam em uma região do cérebro chamada hipocampo, que é a área do cérebro responsável pelos fatos memorizados (idem). Alguns alunos serão mais lentos quando estiverem memorizando, mas ainda terão potencial matemático excepcional. Os fatos matemáticos representam uma parte muito pequena da matemática, mas, infelizmente, os alunos que não os memorizam, em geral, chegam a acreditar que nunca poderão ter sucesso com a matemática e afastam-se da matéria.
Professores em todos os EUA e Reino Unido pedem aos alunos para memorizar fatos matemáticos, e, às vezes, também pedem que memorizem fatos de adição e subtração, geralmente porque os padrões curriculares especificaram que os alunos precisam ser “mais fluentes com os números”. Parish, baseado em Fosnot e Dolk (2001), define a fluência como “saber de que forma um número pode ser composto e decomposto e usar essa informação para ser flexível e eficiente na resolução de problemas”. (PARISH, 2014, p. 159) Independentemente de acreditarmos ou não que a fluência exige mais do que lembrar fatos matemáticos, as pesquisas apontam que: desenvolver o senso numérico e trabalhar com números de formas diferentes, em vez de memorizar cegamente, sem senso numérico, são as melhores maneiras de fortalecer a fluência com os números.
Quando os professores enfatizam a memorização dos fatos, e dão testes para medir fatos numéricos, os alunos sofrem de duas formas. Para cerca de um terço deles, a introdução dos testes cronometrados representa o começo da ansiedade matemática (BOALER, 2014). Sian Beilock e seus colegas estudaram o cérebro humano por meio de ressonância magnética e descobriram que os fatos matemáticos ocorrem na seção em que a memória opera no cérebro. Mas quando os alunos estão estressados, como em situações nas quais estão respondendo a perguntas de matemática sob a pressão do tempo, o funcionamento da memória sofre um bloqueio e os alunos não conseguem acessar os fatos que sabem (BEILOCK, 2011) (RAMIREZ et al, 2013). À medida que eles percebem que não conseguem se sair bem em testes cronometrados, começam a ficar ansiosos e sua confiança na matemática é corroída. O bloqueio do funcionamento da memória e a ansiedade ocorrem particularmente entre as garotas e entre os alunos de desempenho mais alto. Estimativas conservadoras indicam que pelo menos um terço dos alunos passa por situações de estresse extremo em testes cronometrados, não sendo eles (alunos) parte de um grupo de desempenho ou contexto econômico específicos. Quando os submetemos a experiências que geram ansiedade, os alunos fecham as portas para a matemática.
A ansiedade matemática tem sido registrada em alunos a partir dos 5 anos de idade (RAMIREZ et al, 2013) e os testes cronometrados são a maior causa dessa condição debilitante, que às vezes dura por toda a vida. Mas existe uma segunda razão igualmente importante contra os testes cronometrados – eles levam muitos alunos a rejeitar a matemática. Em minhas aulas na Universidade de Stanford, convivo com muitos estudantes de graduação traumatizados com a matemática, apesar de estarem entre os alunos de mais alto adesempenho do país. Quando pergunto o que lhes causou tal aversão, muitos apontam os testes cronometrados no segundo ou terceiro ano como um importante ponto de virada, influenciando sua decisão de que a matemática não era para eles. Alguns desses alunos, principalmente as mulheres, relataram a necessidade de entender com profundidade, o que é um objetivo muito válido, e a sensação de que essa compreensão aprofundada não era valorizada ou oferecida quando os testes cronometrados se tornaram parte da aula de matemática. Eles poderiam ter feito um trabalho mais valoroso em suas aulas de matemática, focando na obtenção do sentido e na compreensão, mas os testes cronometrados evocam emoções tão fortes que os alunos podem vir a acreditar que a essência da matemática está baseada em ser rápido em fatos matemáticos. Isso é extremamente lamentável. Vemos o resultado dessa ênfase equivocada na memorização e aplicação de testes no número de alunos que estão desistindo da matemática e nas crises da matemática que hoje enfrentamos (veja: youcubed.stanford.edu). Quando minha própria filha começou a decorar tabuadas e a fazer testes aos 5 anos de idade na Inglaterra, ela começou a voltar para casa chorando. Essa não é a emoção que desejamos que os alunos associem à matéria e, enquanto continuarmos a colocar os alunos sob pressão para que se lembrem de fatos rapidamente, não eliminaremos a ansiedade disseminada e o desgosto pela matemática que permeiam os EUA e o Reino Unido (SILVA; WHITE, 2014) (NATIONAL NUMERACY, 2014).
Nos últimos anos, os pesquisadores do cérebro descobriram que os alunos que se saem melhor com problemas numéricos são aqueles que usam diferentes rotas cerebrais – uma que seja numérica e simbólica e outra que envolva mais o raciocínio intuitivo e espacial (PARK; BRANNON, 2013). Ao fim deste artigo, oferecemos muitas atividades que estimulam a compreensão visual dos fatos numéricos, para ativar importantes conexões cerebrais. Além disso, os pesquisadores do cérebro analisaram duas maneiras com as quais os alunos estavam aprendendo fatos matemáticos – por meio de estratégias e da memorização. Eles descobriram que as duas abordagens (estratégias ou memorização) envolvem dois caminhos distintos no cérebro e que ambos podem perfeitamente ser usados ao longo da vida. É importante ressaltar, contudo, outra descoberta do estudo: os sujeitos que aprenderam por meio de estratégias alcançaram um “desempenho superior” em relação aos que aprenderam pela memorização; aqueles que resolveram os problemas com a mesma rapidez e mostraram uma melhor transferência para novos problemas. Assim, os pesquisadores do cérebro concluíram que a automaticidade deve ser alcançada por meio da compreensão das relações numéricas e essa, por sua vez, é alcançada por meio do raciocínio acerca das estratégias numéricas (DELAZER et al, 2005).
Por Que a Matemática é Tratada de Modo Diferente?
Para aprender a ser um bom aluno de língua e literatura, a ler e entender romances ou poesias, os alunos precisam ter memorizado o significado de muitas palavras. Mas nenhum aluno dessa matéria diria ou pensaria que o aprendizado se baseia na rápida memorização e lembrança das palavras. Isso se dá porque aprendemos as palavras usando-as em muitas situações diferentes – na fala, na leitura e na escrita. Os professores de língua e literatura não dão aos alunos centenas de palavras para que eles as memorizem e então os testam sob a pressão do cronômetro. Todas as matérias exigem a memorização de alguns fatos, mas a matemática é a única na qual os professores acreditam que os alunos deveriam ser testados sob a pressão do cronômetro. Por que tratamos a matemática dessa forma?
A matemática já tem um imenso problema de imagem. Os alunos raramente choram por causa de outras matérias, tampouco creem que elas sejam baseadas na rapidez e na memorização. As práticas de ensino e o acompanhamento dos pais focados na memorização de fatos matemáticos são em grande medida responsáveis pelo afastamento dos alunos da matemática. Muitas pessoas argumentarão que a matemática é diferente de outras matérias e que ela, simplesmente, precisa ser desse jeito; essa matemática baseia-se, fundamentalmente, em alcançar as respostas certas, não em interpretar e encontrar o significado. Trata-se de outro equívoco. O âmago da matemática é o raciocínio – refletir sobre por que os métodos fazem sentido e falar sobre os motivos para o uso de métodos diferentes (BOALER, 2013). Os fatos matemáticos representam uma pequena parte da matemática, e são, provavelmente, a parte menos interessante. Conrad Wolfram, da Wolfram-Alpha, uma das maiores empresas de matemática do mundo, fala publicamente sobre a amplitude da matemática e a necessidade de pararmos de vê-la como cálculo. Nem Wolfram, nem eu, estamos dizendo que as escolas não devem ensinar cálculo, mas o peso que se dá a ele precisa mudar, e os alunos precisam aprender a calcular por meio do senso numérico, assim como passar mais tempo estudando partes subdesenvolvidas, mas essenciais, da matemática, tais como a resolução de problemas e o raciocínio.
Ao ensinar o senso e os fatos numéricos para os alunos, é importante nunca dar ênfase à rapidez. Na verdade, esse conceito vale para toda a matemática, pois existe um equívoco comum e danoso: a ideia de que alunos bons em matemática são rápidos. Eu trabalho com muitos matemáticos e percebo que eles não são, particularmente, rápidos com números. Na verdade, alguns deles são um tanto lentos. Isso não é algo ruim. Eles são lentos porque pensam profunda e cuidadosamente sobre matemática. Laurent Schwartz, um grande matemático, escreveu uma autobiografia sobre sua época de escola e como o fizeram se sentir “burro” por ser um dos mais lentos em matemática de sua turma (SCHWARTZ, 2001). Ele passou muitos anos sentindo-se inadequado até chegar à conclusão que “a rapidez não tem uma relação precisa com a inteligência. O importante é compreender profundamente as coisas e suas relações umas com as outras. É aí que está a inteligência. Ser rápido ou devagar realmente não é muito relevante” (idem). Infelizmente, as aulas de matemática baseadas na rapidez e nos testes levam muitos alunos lentos e reflexivos, como Schwartz, a crer que não podem se sair bem na matéria.
A “Fluência” em Matemática e o Currículo
Nos EUA, o currículo do Common Core (CCSS) estabelece a “fluência” como objetivo. Ela surge quando os alunos desenvolvem senso numérico e confiam em suas habilidades com a matemática, pois entendem os números. Lamentavelmente, a palavra fluência é quase sempre mal interpretada. O “Engage New York” é um currículo que está se tornando cada vez mais popular nos EUA, e tem, erroneamente, interpretado fluência da seguinte maneira:
Fluência: Espera-se que os alunos sejam rápidos e precisos em cálculos simples; os professores estruturam o tempo de aula e/ou lição de casa para que os alunos memorizem, por meio de repetição, funções nucleares como tabuadas de multiplicação. Assim, eles são mais capazes de entender e manipular funções mais complexas. (Engage New York)
Há muitos problemas nessa diretiva. A rapidez e a memorização são duas orientações das quais precisamos nos afastar com urgência, em vez de ir em sua direção. De forma não menos problemática, o “Engage New York” conecta a memorização de fatos numéricos à compreensão dos alunos de funções mais complexas, o que nunca foi provado por pesquisas. O que elas, de fato, nos dizem é que os alunos entendem funções mais complexas quando têm senso numérico e profunda compreensão de princípios numéricos e não quando memorizam cegamente ou se lembram rapidamente (BOALER, 2009). No momento, estou trabalhando com analistas do PISA na OECD. A equipe do PISA não apenas emite testes internacionais de matemática a cada 4 anos, mas coleta dados sobres as estratégias matemáticas dos alunos. Seus dados sobre 13 milhões de adolescentes de 15 anos de todo o mundo mostram que os alunos de desempenho mais baixo são aqueles que focam na memorização e acreditam que ela é importante para estudar matemática (BOALER; ZOIDO, no prelo). Essa ideia começa a ser incutida cedo nas salas de aula, e precisa ser erradicada. Os alunos de alto desempenho no mundo são aqueles que focam em ideias fundamentais de matemática e nas conexões entre as ideias. Os alunos desenvolvem uma visão conectada da matemática quando trabalham nela de forma conceitual e a memorização cega é substituída pela construção do sentido.
No Reino Unido, as diretivas têm o mesmo potencial danoso. O novo currículo nacional estabelece que, aos nove anos de idade, todos os alunos devem “ter memorizado a tabuada de multiplicação até o número 12” e, embora os alunos possam memorizar fatos multiplicativos até (12 x 12) por meio de atividades ricas e engajadoras, essa diretiva está levando os professores a fazer os alunos memorizarem tabuadas de multiplicação, para depois testá-los. Um grupo importante no Reino Unido, liderado pelo autor de livros infantis e poeta Michael Rosen, formou-se para destacar o quanto as atuais políticas nas escolas são nocivas, bem como o número de crianças do ensino fundamental que agora voltam para casa chorando devido ao estresse a que são submetidas, causado pelo excesso de testes (GARNER, 2014). A matemática é a maior causadora de ansiedade e medo nos alunos e o foco desnecessário na memorização de fatos matemáticos nos primeiros anos da vida escolar é uma das principais razões.
Atividades para Desenvolver Fatos e Senso Numérico
Os professores devem ajudar os alunos a desenvolver fatos matemáticos, encorajando-os a usar e explorar os números, assim como a trabalhar com eles, ao invés de mera ênfase nos fatos ou no uso de “testes cronometrados”. Quando os alunos executam atividades numéricas significativas, memorizam fatos matemáticos ao mesmo tempo em que compreendem os números e a matemática. Em vez de memorizar e ter horror à matemática, eles apreciam e aprendem uma matemática significativa.
Conversas Numéricas
A estratégia de ensino chamada “conversas numéricas”, desenvolvida por Ruth Parker e Kathy Richardson, é um dos melhores métodos para ensinar o senso numérico e os fatos matemáticos ao mesmo tempo. Essa é uma atividade curta de ensino ideal, que pode ser usada pelos professores para iniciar a aula, ou pelos pais, em casa. Ela envolve apresentar um problema abstrato de matemática, tal como (18 x 5), e pedir aos alunos que resolvam o problema mentalmente. Depois, o professor coleta os diferentes métodos e observa por que funcionam. Ele pode, por exemplo, apresentar (18 x 5) e descobrir que os alunos resolveram o problema destas diferentes maneiras:
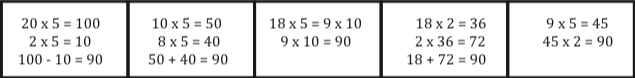
Os alunos adoram compartilhar suas diferentes estratégias e, geralmente, ficam completamente engajados e fascinados com os diferentes métodos que surgem. Eles aprendem a matemática mental, têm oportunidades de memorizar fatos matemáticos e também desenvolvem a compreensão conceitual dos números e das propriedades aritméticas essenciais para ter sucesso na álgebra e em outras operações. Os pais podem usar uma estratégia similar, pedindo aos filhos que compartilhem seus métodos, e em seguida discutindo os diferentes métodos que podem ser usados. Dois livros, um de Cathy Humphreys e Ruth Parker (no prelo), e outro de Sherry Parish (2014) ilustram as muitas e diferentes conversas sobre números com as quais se pode trabalhar com alunos do ensino médio e fundamental, respectivamente.
As pesquisas nos dizem que as melhores salas de aula de matemática são aquelas nas quais os alunos aprendem fatos matemáticos e o senso numérico por meio do engajamento em atividades que focam na compreensão da matemática, em vez da memorização pela repetição.
As cinco atividades a seguir foram escolhidas para ilustrar esse princípio.
Atividades com Fatos de Adição
 Estalar!: Esta é uma atividade que as crianças podem fazer em grupos. Cada criança deve montar um trem com um número especificado de cubos. Quando o professor disser “Estalar!”, as crianças dividem seus trens em duas partes e colocam uma mão atrás das costas. Em seguida, elas se revezam dando a volta no círculo e mostrando seus cubos restantes. As outras crianças devem descobrir o número completo da combinação.
Estalar!: Esta é uma atividade que as crianças podem fazer em grupos. Cada criança deve montar um trem com um número especificado de cubos. Quando o professor disser “Estalar!”, as crianças dividem seus trens em duas partes e colocam uma mão atrás das costas. Em seguida, elas se revezam dando a volta no círculo e mostrando seus cubos restantes. As outras crianças devem descobrir o número completo da combinação.
Por exemplo, se o meu trem tem 8 cubos, eu poderia estalar três cubos e escondê-los atrás das minhas costas. Eu mostraria ao meu grupo os 5 cubos que sobraram e, em resposta, eles devem dizer que 3 estão faltando, e que 5 e 3 somam 8.
Quantos Estão Escondidos? Nessa atividade, cada criança tem o mesmo número de cubos e uma caneca. Elas se revezam escondendo alguns dos seus cubos na caneca e mostrando os restantes. As outras crianças devem calcular a resposta da pergunta: “Quantos Estão Escondidos?”, e dizer a combinação completa dos números.
Exemplo: Eu tenho 10 cubos e decido esconder 4 na minha caneca. Meu grupo pode ver que eu só tenho 6 cubos. Os alunos devem dizer que eu estou escondendo 4 cubos, e que 6 e 4 somam 10.
Atividades de Fatos Multiplicativos
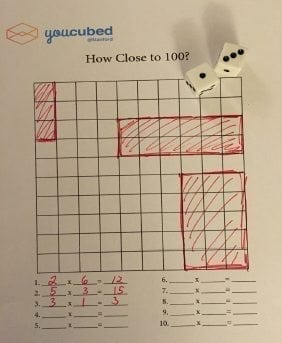 Quão perto de 100? Este jogo deve ser jogado em pares. Duas crianças compartilham uma grade em branco numa folha de papel, com 100 casas. O primeiro jogador lança dois dados. Os números que saírem são os que a criança usa para preencher um conjunto na grade. Elas podem colocar o conjunto onde quiserem, mas o objetivo é preencher a grade inteira o mais rápido possível. Depois de o jogador preencher o conjunto na grade, deve, em seguida, escrever a sentença numérica correspondente. O jogo termina quando ambos jogadores tiverem lançado os dados e não conseguirem mais colocar nenhum conjunto na grade.
Quão perto de 100? Este jogo deve ser jogado em pares. Duas crianças compartilham uma grade em branco numa folha de papel, com 100 casas. O primeiro jogador lança dois dados. Os números que saírem são os que a criança usa para preencher um conjunto na grade. Elas podem colocar o conjunto onde quiserem, mas o objetivo é preencher a grade inteira o mais rápido possível. Depois de o jogador preencher o conjunto na grade, deve, em seguida, escrever a sentença numérica correspondente. O jogo termina quando ambos jogadores tiverem lançado os dados e não conseguirem mais colocar nenhum conjunto na grade.
Pizza de Calabresa: Neste jogo, as crianças lançam o dado duas vezes. O primeiro lance informa quantas pizzas desenhar. O segundo informa quantas fatias de calabresa colocar em CADA pizza. Depois, eles escrevem a sentença numérica que lhes ajudará com a pergunta: “Quantas fatias de calabresa todas as pizzas têm no total?”
Por exemplo, eu lanço o dado e sai o número 4, então, desenho 4 grandes pizzas. Jogo o dado de novo e sai o número 3, então, eu coloco três fatias de calabresa em cada pizza. Depois, escrevo (4 x 3 = 12) e isso me diz que há 12 fatias de calabresa no total.
Cartas de Matemática
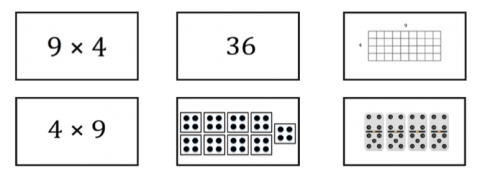
Muitos pais usam as “cartas” como uma forma de encorajar o aprendizado de fatos matemáticos. Elas geralmente incluem duas práticas inúteis: a memorização sem a compreensão e a pressão do tempo. Em nossa atividade de Cartas de Matemática usamos a estrutura das cartas, de que as crianças gostam, mas colocamos a ênfase no senso numérico e na compreensão da multiplicação. O objetivo da atividade é combinar as cartas com a mesma resposta numérica, exibida por meio de diferentes representações. Coloque todas as cartas na mesa e peça às crianças para pegá-las uma de cada vez; elas podem pegar todas as que encontrarem com a mesma resposta (demonstrada por qualquer representação). Por exemplo, 9 e 4 podem ser mostrados com um modelo de área, conjuntos de objetos como dominós, e uma sentença numérica. Quando os alunos combinam as cartas, devem explicar como acham que as cartas diferentes são equivalentes. Esta atividade estimula o entendimento da multiplicação e é também uma repetição dos fatos matemáticos.
Conclusão: Conhecimento é Poder
As atividades mostradas acima são ilustrações de jogos e tarefas nos quais os alunos aprendem fatos matemáticos ao mesmo tempo em que trabalham com algo que lhes dá prazer, em vez de algo que temem. As diferentes atividades também focam na compreensão da adição e multiplicação, em vez da memorização cega. Isso é extremamente importante.
Como educadores, todos temos em comum o objetivo de estimular aprendizes poderosos, que pensam cuidadosamente a matemática, e usam os números com fluência. No entanto, os professores e responsáveis pelo desenvolvimento dos currículos geralmente não conseguem acessar pesquisas importantes e isso tem significado a continuação de práticas improdutivas e contraproducentes em sala de aula. Este artigo ilustra o dano causado por práticas que, geralmente, acompanham o ensino de fatos matemáticos – pressão por velocidade, testes cronometrados e memorização cega – e resume resultados de pesquisa que evidenciam algo muito diferente: o senso numérico. Alunos de alto desempenho usam o senso numérico e é fundamental que alunos com baixo desempenho também aprendam a usar os números de forma flexível e conceitual, em vez de executar exercícios de repetição e memorização. A memorização e os testes cronometrados são um empecilho para o senso numérico, dando aos alunos a impressão de que fazer sentido não é importante. Precisamos com urgência reorientar nosso ensino dos números e do senso numérico no Reino Unido e nos EUA. Se isso não ocorrer, a taxa de repetências e desistências – que já estão em níveis recorde em ambos países (NATIONAL NUMERACY, 2004) (SILVA; WHITE, 2013) – vão aumentar. Quando enfatizamos a memorização e o sistema de testes em nome da fluência, estamos prejudicando as crianças, arriscando o futuro de nossa sociedade cada vez mais quantitativa e ameaçando a disciplina da matemática. Temos o conhecimento científico do que precisamos para mudar isso, e para permitir que todas as crianças sejam poderosas aprendizes de matemática. Agora, está na hora de usá-lo.
Referências
Beilock, S. (2011). Choke: What the Secrets of the Brain Reveal About Getting It Right When You Have To. New York: Free Press.
Boaler, J. (2015). What’s Math Got To Do With It? How Teachers and Parents Can Help Transform Mathematics Learning and Inspire Success. New York: Penguin.
Boaler, J. (2013, Nov 12 2013). The Stereotypes That Distort How Americans Teach and Learn Math. The Atlantic.
Boaler, J. & Zoido, P. (in press). The Impact of Mathematics Learning Strategies upon Achievement: A Close Analysis of Pisa Data.
Delazer, M., Ischebeck, A., Domahs, F., Zamarian, L., Koppelstaetter, F., Siedentopf, C.M. Kaufmann; Benke, T., & Felber, S. (2005). Learning by Strategies and Learning by Drill – evidence from an fMRI study. NeuroImage. 839-849
Engage New York. https://schools.nyc.gov/NR/rdonlyres/9375E046-3913-4AF5-9FE3-D21BAE8FEE8D/0/CommonCoreIn- structionalShifts_Mathematics.pdf
Feikes, D. & Schwingendorf, K. (2008). The Importance of Compression in Children’s Learning of Mathematics and Teacher’s Learning to Teach Mathematics. Mediterranean Journal for Research in Mathematics Education 7 (2).
Fosnot, C, T & Dolk, M (2001). Young Mathematicians at Work: Constructing Multiplication and Division. Heinemann:
Garner, R. (October 3, 2014). The Independent. ( Link to Article )
Gray, E., & Tall, D. (1994). Duality, Ambiguity, and Flexibility: A “Proceptual” View of Simple Arithmetic. Journal for Research in Mathematics Education, 25(2), 116-140.
Humphreys, Cathy & Parker, Ruth (in press). Making Number Talks Matter: Developing Mathematical Practices and Deepen- ing Understanding, Grades 4-10. Portland, ME: Stenhouse.
LA Times (1990) https://articles.latimes.com/1990-05-10/news/mn-1461_1_math-error
Parish, S. (2014). Number Talks: Helping Children Build Mental Math and Computation Strategies, Grades K-5, Updated with Common Core Connections. Math Solutions.
Park, J. & Brannon, E. (2013). Training the Approximate Number System Improves Math Proficiency. Association for Psychological Science, 1-7
Ramirez, G., Gunderson, E., Levine, S., and Beilock, S. (2013). Math Anxiety, Working Memory and Math Achievement in Early Elementary School. Journal of Cognition and Development. 14 (2): 187–202.
Supekar, K.; Swigart, A., Tenison, C., Jolles, D., Rosenberg-Lee, M., Fuchs, L., & Menon, V. (2013). Neural Predictors of Indi- vidual Differences in Response to Math Tutoring in Primary-Grade School Children. PNAS, 110, 20 (8230-8235)
Schwartz, L. (2001). A Mathematician Grappling with His Century. Birkhäuser
Silva, E., & White, T. (2013). Pathways to Improvement: Using Psychological Strategies to help College Students Master Devel- opmental Math: Carnegie Foundation for the Advancement of Teaching.
National Numeracy (2014). https://www.nationalnumeracy.org.uk/what-the-research-says/index.html
