Introdução
Sou fascinada pela maneira complexa como as crianças entendem a matemática. Elas fazem perguntas, veem ideias, desenham representações, conectam métodos, apresentam justificativas e raciocinam de inúmeras formas. Mas, nos últimos anos, essa complexidade com diferentes nuance relativas ao aprendizado foi reduzida a números e letras usados para julgar o valor dos alunos. Os professores são incentivados a avaliá-los e classificá-los a um nível ridículo e prejudicial, pois os estudantes começam a se definir − e a definir a matemática − em termos de letras e números. Tais representações grosseiras da compreensão matemática fornecem, em grande medida, uma descrição deficiente e, em muitos casos, falsa do conhecimento das crianças.
Nos Estados Unidos, os estudantes são testados em demasia, a um nível nada menos que gritante, particularmente no campo da matemática. Há muitos anos eles têm sido julgados por meio de perguntas estreitas e procedimentais, apresentadas com respostas de múltipla escolha. O conhecimento necessário para ter um bom desempenho em testes como esse está tão distante do raciocínio adaptável, crítico e analítico de que os alunos precisam no mundo moderno que grandes empregadores, como o Google, declararam não ter mais interesse nas notas durante o processo seletivo porque elas não servem como parâmetro de sucesso no ambiente de trabalho (BRYANT, 2013).
Um princípio crucial de um bom método de testes é avaliar o que importa.
Há muitas décadas, nos Estados Unidos, os testes têm avaliado o que pode ser testado com facilidade, em detrimento da matemática que realmente importa e tem valor. Isso significa que os professores precisam focar na estreita matemática procedimental, e não na matemática ampla, criativa e expansiva, que é tão importante. As novas avaliações do Common Core1 prometem algo diferente, com poucas perguntas de múltipla escolha e testes de resolução de problemas. No entanto, elas têm sido recebidas pelos pais com uma considerável objeção.
Pôr um fim aos testes padronizados não significa erradicar os danos que eles podem causar, pois muitos professores acreditam que devem usar testes similares a avaliações padronizadas, mesmo quando sabem que elas avaliam uma matemática limitada.
Eles fazem isso com o intuito de ajudar a preparar os alunos a ter um bom desempenho no futuro. Alguns professores, em especial no Ensino Médio, chegam a aplicar testes semanais, ou até mais frequentes. Quem ensina matemática, mais do que os docentes de outras disciplinas, acha que é preciso avaliar os alunos regularmente. Isso acontece porque eles foram levados a crer que a matemática se resume ao desempenho, e acabam não considerando o papel dos testes em moldar a forma como os alunos olham a matemática e a si mesmos. Muitos professores que conheço aplicam testes no primeiro dia de aula, o que logo de partida transmite à classe uma forte mensagem sobre o desempenho, justo quando é tão importante dar mensagens edificantes sobre a matemática e o aprendizado.
A Finlândia é um dos países com os melhores resultados do mundo em testes internacionais de matemática. Lá os alunos não fazem testes na escola. Em vez disso, os professores usam sua rica compreensão do adquirido nas aulas para dar feedback aos pais e julgar o trabalho dos estudantes. Em uma pesquisa longitudinal que fiz na Inglaterra, os alunos trabalharam com projetos abertos por três anos (dos 13 anos aos 16 anos), até chegar a hora dos exames padronizados nacionais. Durante esse período, eles não fizeram provas e seu trabalho tampouco recebeu nota. Nas últimas semanas antes dos exames, os professores deram às turmas testes com perguntas curtas que avaliavam procedimentos. Apesar de os alunos não terem familiaridade com perguntas de exames, ou de tampouco terem trabalhado sob a pressão do cronômetro, seu desempenho foi significativamente melhor do que um grupo de mesmo nível que passara três semanas respondendo questões similares às do exame nacional e sendo frequentemente submetidos a testes (BOALER, 1998, 2015). O motivo pelo qual os alunos da escola de resolução de problemas se saíram tão bem nos exames nacionais se dá porque eles haviam aprendido a acreditar em seu potencial, recebido informações úteis e diagnósticas sobre seu aprendizado e descoberto que eram capazes de resolver qualquer questão, uma vez que estavam habituados a solucionar problemas matemáticos.
Estudantes sem nenhuma experiência com exames e testes podem ter resultados excepcionais, pois a preparação mais importante que podemos dar é uma mentalidade aberta para o desenvolvimento do raciocínio2; crenças positivas e ferramentas de resolução de problemas que vão equipá-los para qualquer situação matemática.
O regime de testes da última década teve um forte e negativo impacto sobre os alunos, mas esse não é o único problema; a forma como as notas são comunicadas é igualmente ruim. Quando os alunos recebem uma porcentagem ou nota, não há muito o que fazer, exceto compará-las com aqueles a seu redor, e, nesse processo, metade deles, ou mais, conclui que não é tão bom quanto os outros. Isso é conhecido como “feedback de ego”, forma comprovadamente danosa ao aprendizado. Infelizmente, quando os alunos recebem seus resultados nos testes, começam a se ver como notas e pontuações. Não consideram as pontuações como um indicativo de seu aprendizado ou do que eles precisam fazer para melhorar, mas indicativos de quem são como pessoas. O fato de que os estudantes dos Estados Unidos comumente descrevem a si mesmos dizendo “sou um aluno nota 10”, ou “sou um aluno nota 5”, ilustra como eles se definem por meio de notas. Ray McDermott escreveu um convincente artigo sobre o aprisionamento de uma criança numa deficiência de aprendizado, descrevendo como as formas diferentes como um aluno pensa e trabalha são rotuladas e então definidas por meio desses rótulos (MCDERMOTT, 1993). Eu poderia oferecer um argumento parecido sobre o quanto notas e pontuações em testes são limitantes.
Os alunos se descrevem por meio de notas como 10 ou 5 porque cresceram numa cultura do desempenho que valoriza os testes frequentes e a avaliação por notas, em vez da persistência, da coragem e da capacidade de resolução de problemas. Os métodos tradicionais de avaliação usados há décadas nos Estados Unidos foram concebidos em uma época menos esclarecida (KOHN, 2011), em que se acreditava que as notas e pontuações motivariam os alunos, e que as informações fornecidas por elas sobre desempenho seriam úteis.
Hoje sabemos que as notas e pontuações desmotivam os alunos, em vez de motivá-los, e transmitem mensagens fixas e prejudiciais que resultam numa piora do aproveitamento nas salas de aula.
Em estudos sobre a atribuição de notas e alternativas a esse método, os pesquisadores apresentaram resultados sólidos. Inúmeros trabalhos mostram que o ato de atribuir notas afeta de forma negativa o desempenho dos alunos. Elawar e Corno, por exemplo, compararam as formas como os professores produziram respostas a lições de casa de alunos do 6º ano − metade deles recebeu notas, e a outra metade, comentários diagnósticos sem nota (ELAWAR; CORNO, 1985). Aqueles que receberam comentários aprenderam duas vezes mais rápido que o grupo de controle, as diferenças de desempenho entre meninos e meninas desapareceram e a atitude dos alunos melhorou.
Um estudo de Ruth Butler acrescentou uma terceira condição, que deu aos alunos notas e comentários − pois esse poderia ser considerado o melhor dos dois cenários (BUTLER, 1987,1988). Nesse estudo, os alunos que receberam somente notas e os que receberam notas e comentários tiveram resultados igualmente ruins; o grupo que havia recebido apenas comentários, no entanto, obteve um desempenho significativamente melhor. Isso mostra que, quando os alunos receberam uma nota e um comentário, eles se focaram apenas nas notas. Butler descobriu que, em comparação àqueles que receberam apenas comentários diagnósticos, tanto os alunos do quinto quanto do sexto ano de alto (os 25% com a melhor média de notas) e baixo (os 25% com a pior média de notas) aproveitamento sofreram déficits em seu desempenho e motivação em ambas as condições que incluíam notas. Outras pesquisas mostraram que foi só os estudantes pensarem que faziam um trabalho que valia nota para perderem a motivação, o que acabou resultando em níveis mais baixos de desempenho (PULFREY; BUCHS; BUTERA; 2011).
A transição das notas para os comentários diagnósticos é crucial, pois se trata de uma mudança que permite aos professores dar um incrível presente aos alunos − o conhecimento e insights importantes que os ajudarão a melhorar seu desempenho.
Os educadores preocupam-se, e com razão, com o trabalho extra que isso vai dar, pois muitos professores já excedem, sobremaneira, as horas que são pagos para trabalhar. A solução que recomendo é avaliar menos. Se a atribuição de notas semanais fosse substituída por ocasionais comentários diagnósticos, haveria investimento na mesma carga de tempo, mas eliminando mensagens que transmitem mentalidades fixas e oferecendo aos alunos insights que poderiam impulsioná-los a traçar caminhos em direção a um desempenho melhor. Quem fez essas mudanças percebeu que houve melhoras de desempenho nos testes, ou nenhuma alteração, e um aumento significativo da motivação e da confiança.
Quando damos avaliações aos alunos, criamos uma oportunidade importante. Tarefas e perguntas bem desenvolvidas, acompanhadas por um feedback claro, oferecem aos alunos um caminho de crescimento que os ajuda a ter consciência de que o aprendizado pode chegar a níveis altíssimos, e, principalmente, a saber como eles podem chegar lá. Infelizmente, a maioria dos sistemas de avaliação das salas de aula dos Estados Unidos faz o oposto, transmitindo informações que levam muitos estudantes a pensar que são um fracasso e jamais conseguirão aprender matemática. Nos últimos anos, tenho trabalhado com professores que mudaram seus métodos de avaliação, abandonando testes-padrão com notas e pontuações e abraçando avaliações focadas em dar aos alunos as informações de que precisam para aprender, bem acompanhadas de mensagens que expressam uma é mentalidade aberta para o desenvolvimento do raciocínio. Isso resultou em grandes mudanças no ambiente de suas salas de aula.
Quando damos avaliações aos alunos, criamos uma oportunidade importante. Tarefas e perguntas bem desenvolvidas, acompanhadas por um feedback claro, oferecem aos alunos um caminho de crescimento que os ajuda a ter consciência de que o aprendizado pode chegar a níveis altíssimos, e, principalmente, a saber como eles podem chegar lá.
Sou ferrenha defensora dos professores e sei que a era do programa No Child Left Behind3 arruinou o profissionalismo e o entusiasmo de muitos deles, que se viram forçados (e estou ciente do peso dessa palavra) a usar métodos de ensino que eles sabiam ser improdutivos. Atualmente, parte importante do meu trabalho com professores é ajudá-los a recuperar seu senso de profissionalismo. O meu objetivo é ajudá-los a ver a si mesmos como criadores novamente, como pessoas que podem criar ambientes de ensino permeados pelas próprias ideias para uma matemática arrojada e envolvente. Tenho observado que os professores ganham um novo fôlego quando são estimulados nessas novas maneiras de trabalhar e avaliar.
No novo filme de Vicki Abeles, diretora de Race to Nowhere (assista ao trailer para saber mais), sua equipe entrevistou alunos das séries finais do Ensino Fundamental no distrito em que eu estava trabalhando para ajudar os professores a mudar sua forma de ensino e avaliação. No filme, uma garota, Delia, diz que sempre recebia notas baixas em suas lições de casa no ano anterior, e que, por isso, acabou deixando de persistir na matemática e, surpreendentemente, em todas as outras matérias na escola. Em sua entrevista, ela explica de um jeito comovente:
“Quando eu via a nota 4 no papel, era como se eu fosse um nada. Achei que eu ia me sair mal em todo o resto porque estava indo mal naquela disciplina. Então, eu nem sequer me dei ao trabalho de tentar”. Mais adiante, ela fala sobre as mudanças em sua aula de matemática e como ela agora se sente estimulada a ter um bom desempenho. “Eu odiava matemática”, explica. “Odiava com todas as minhas forças, mas agora me sinto conectada a ela; estou aberta, me sinto viva, tenho mais energia.”

O fato de Delia ter usado a palavra “aberta” ao descrever como se sentia em relação à matemática é algo que, muitas vezes, escuto dos estudantes quando assistem aulas sem o medo iminente de notas e pontuações baixas. Mas isso vai além da avaliação − quando ensinamos uma matemática criativa e investigativa, os alunos adquirem uma poderosa liberdade intelectual. Em entrevistas com alunos do 3º ano do Ensino Fundamental que haviam tido conversas numéricas em sala, pergunto como se sentem em relação a elas. A primeira coisa que o jovem Dylan disse na entrevista foi: “Eu me sinto livre.” Ele então descreveu como a valorização de diferentes estratégias matemáticas lhe permitiu ter a sensação de que poderia trabalhar com a matéria do jeito que quisesse, explorar ideias e aprender sobre os números. O uso de palavras como “livre” e “aberto” demonstram que, quando os alunos trabalham com uma mentalidade aberta para o desenvolvimento do raciocínio, isso faz uma grande diferença, que vai muito além do desempenho na matemática e alcança o empoderamento intelectual que afetará os alunos por toda a vida (BOALER, 2015).
As percepções que os alunos adquirem em relação ao próprio potencial afetam o aprendizado e o desempenho, bem como a motivação e o esforço, que são igualmente importantes − como Delia descreve no filme. Quando ela tirou uma nota baixa em matemática, desistiu não só dessa matéria, mas de todas as outras, sentindo-se um fracasso. Essa não é uma resposta incomum ao método de notas.
Quando os alunos recebem notas mostrando que sua posição está abaixo da de alguns outros, eles geralmente desistem da escola, pois concluem que nunca vão conseguir aprender e assumem a postura de um aluno com mau desempenho.
Dar notas e pontuações a quem tem alto aproveitamento é igualmente prejudicial, pois eles passam a acreditar que são “Nota 10” e enveredam num precário ambiente de aprendizado imbuído de uma mentalidade fixa que os faz evitar trabalhos que exijam maior empenho ou desafios por temerem perder esse rótulo. Estudantes assim ficam arrasados quando recebem uma nota 8, ou menos, em qualquer trabalho seu.
Em outro estudo sobre a atribuição de notas, Deevers descobriu que os alunos que não recebiam pontuações, mas feedbacks construtivos apresentavam melhor desempenho em seu trabalho futuro. Infelizmente, ele também descobriu que, à medida que os alunos cresciam, os professores davam cada vez menos feedback construtivo e atribuíam mais notas de forma fixa. O pesquisador percebeu a clara e pouco surpreendente relação entre as práticas avaliativas dos professores e a atitude dos alunos, pois a opinião que tinham do próprio potencial e da possibilidade de melhorar o aprendizado piorou do 5º ao 2º ano do Ensino Médio (DEEVERS, 2006).
Queremos que os alunos fiquem empolgados e interessados pelo que estão aprendendo, pois, quando isso acontece, a motivação deles aumenta e seu desempenho melhora. Há um grande número de pesquisas que estudaram dois tipos de motivação: a intrínseca, que vem do interesse na matéria e nas ideias que se está aprendendo; e a extrínseca, oferecida pela sensação de receber as melhores notas e pontuações. Pela matemática ter sido há décadas ensinada como uma matéria de desempenho, os alunos mais empenhados nas aulas, muitas vezes, são aqueles cuja motivação é extrínseca. Um dos resultados disso é que quem tem uma relação positiva com as aulas geralmente tira as melhores notas. A maioria dos professores que acredita em notas faz uso delas por acreditar que impulsionam os alunos a ter um bom desempenho. De fato, elas estimulam alguns estudantes – os que, de todo modo, provavelmente, se saem bem em níveis mais altos −, mas acabam desmotivando todos os outros. Infelizmente, a motivação extrínseca adquirida por quem tem alto aproveitamento não funciona a longo prazo. Vários estudos mostram que, comparados aos alunos com motivação extrínseca, os que desenvolvem motivação intrínseca se saem melhor em tarefas de alta complexidade (PULFREY; BUCHS; BUTERA, 2011; LEMOS; VERÍSSIMO, 2014). Eles também apontam que a motivação intrínseca para aprender estimula os alunos a aprofundarem-se nas matérias e continuarem a estudá-las, em vez de abandoná-las.
A avaliação para o aprendizado
Há alguns anos, dois professores ingleses − Paul Black e Dylan Wiliam − conduziram uma meta análise de centenas de pesquisas sobre avaliações. Eles descobriram algo incrível: uma forma de avaliação tão poderosa que, se os professores a usassem, geraria um impacto grande o suficiente para melhorar o desempenho do país em testes internacionais − catapultando-o de uma posição mediana aos cinco melhores. (Sir Paul Black e o professor Dylan Wiliam eram bons colegas meus na Universidade de Londres; Paul Black também foi meu mentor e orientador da minha dissertação.) Black e Wiliam descobriram que, se os professores usassem o que agora é chamado de Avaliação para o Aprendizado, o impacto positivo seria muito maior do que outras iniciativas educacionais, como a redução do tamanho das turmas (BLACK; HARRISON; LEE; MARSHALL; WILLIAM, 1998a, 1998b). Eles publicaram suas descobertas em um pequeno folheto que, logo nas primeiras semanas, vendeu mais de 20 mil cópias na Inglaterra. A Avaliação para o Aprendizado é hoje uma iniciativa nacional em muitos países, cuja enorme base de evidências transmite mensagens de mentalidade aberta para o desenvolvimento do raciocínio aos alunos.
Será útil oferecer agora um pouco de contexto. Existem dois tipos de avaliação − formativa e somativa. A avaliação formativa influencia o aprendizado e é a essência do método da avaliação para o aprendizado, ou A4L4. Esse tipo de avaliação é usado para descobrir em que ponto do aprendizado os alunos estão, dado que vai determinar aos professores e alunos o que eles precisam saber em seguida. A finalidade da avaliação somativa, por outro lado, é a de resumir o aprendizado de um aluno − para dar um relato final sobre o quanto ele avançou, como um ponto de chegada. Um problema nos Estados Unidos é que muitos professores usam a avaliação somativa de maneira formativa; isto é, dão aos alunos uma pontuação final quando eles ainda estão aprendendo o conteúdo. Nas aulas de matemática, os professores, muitas vezes, usam testes somativos semanalmente e, depois, passam para o assunto seguinte; não esperam para ver o que o teste revela. No A4L, os alunos descobrem o que sabem, o que precisam saber, e as maneiras para diminuir a distância entre esses dois pontos. Além disso, recebem informações sobre suas rotas de aprendizado flexíveis e expansíveis, que contribuem para o desenvolvimento de uma mentalidade aberta ao desenvolvimento do raciocínio. Nas semanas e meses em que os alunos estão aprendendo em um curso, é muito importante avaliá-los de maneira formativa e não somativa, o que pode ser feito de muitas maneiras.
Um princípio importante do A4L é que ele ensina os alunos a assumir a responsabilidade por seu próprio conhecimento.
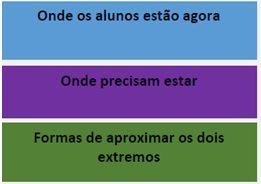
Em essência, o A4L baseia-se no empoderamento dos alunos para que se tornem aprendizes autônomos capazes de autorregular e determinar o que é mais importante para aprender e que conhecem formas de melhorar seu aprendizado. Pode-se dizer que esse modelo de avaliação possui três partes: (1) comunicar com clareza o que foi aprendido; (2) ajudar os alunos a tornarem-se conscientes do ponto em que estão na jornada do aprendizado e onde eles precisam chegar; e (3) dar aos alunos informações sobre como aproximar o ponto em que estão agora e o ponto em que precisam estar.
Desenvolvendo a autoconsciência e a responsabilidade nos alunos
Os aprendizes com mais recursos são reflexivos, engajados na meta cognição (ou seja, eles refletem sobre o que sabem) e assumem o controle do próprio aprendizado (WHITE; FREDERIKSEN, 1998). Um grande defeito das aulas de matemática tradicionais é que os alunos raramente têm ideia do que estão aprendendo ou em que ponto estão em um panorama de aprendizado mais amplo. Eles focam em métodos de memorização, porém, muitas vezes, nem sequer sabem em que área da matemática estão se concentrando. Já visitei muitas aulas de matemática e me aproximei das mesas dos alunos para perguntar sobre o quê, exatamente, eles estavam trabalhando. Em muitos casos, ouvi respostas para a pergunta sobre a qual eles estavam debruçados. Muitas das minhas interações foram algo assim:
JB: − O que você está fazendo?
Aluno(a): − Exercício 2.
JB: Mas o que exatamente você está fazendo? Em que área da matemática está trabalhando?
Aluno(a): − Ah, desculpa: na pergunta 4.
Muitas vezes, os alunos não estão pensando sobre a área da matemática em que estão debruçados, não fazem ideia dos objetivos para seu aprendizado e esperam ser passivamente guiados pelos professores, que lhes dizem quando estão “acertando” ou não. Alice White, especialista em avaliações, compara essa situação a de trabalhadores em um barco, que recebem trabalhos diariamente, mas não têm ideia de onde o barco está nem para onde estão indo.
Uma pesquisa, conduzida por Barbara White e John Frederikson (1998), ilustra de forma poderosa a importância da reflexão. Os investigadores estudaram 12 turmas do 7º ano que estavam aprendendo física e os dividiram entre grupos experimentais e de controle. Todos os grupos receberam aulas sobre força e movimento. Depois, os grupos de controle passaram parte de cada aula discutindo o trabalho, enquanto o experimental ficou engajado em auto avaliações e avaliações dos outros colegas. Os resultados do estudo foram gritantes. Os grupos experimentais tiveram um desempenho melhor que os grupos de controle em três avaliações diferentes.
Inclusive, aqueles com aproveitamento baixo foram os principais beneficiados. Depois de passarem algum tempo refletindo sobre os critérios científicos e se auto avaliando com base neles, o desempenho desse grupo começou a se equiparar ao dos alunos com alto aproveitamento. Os estudantes do 7º ano até se saíram melhor do que pessoas no curso de Física avançada nos testes do Ensino Médio. Assim, os pesquisadores concluíram que grande parte da performance ruim não está vinculada à falta de habilidade, mas ao desconhecimento sobre as áreas que deveriam receber mais foco.
A mesma situação ocorre com muitos alunos, o que demonstra a importância de comunicar o que eles devem aprender, pois isso tanto os ajuda a saber em que um bom desempenho de fato se baseia quanto a começar um processo de reflexão que representa uma inestimável ferramenta para o aprendizado.
Há muitas estratégias para estimular os alunos a se tornarem mais conscientes da matemática que estão aprendendo e o seu papel no processo de aprendizado. Muitas delas estão no próximo livro de Jo, Mathematical Mindsets.
Conclusão
Os testes e as notas podem levar as turmas a se desencantarem com a matemática e até com a escola em si. A Avaliação para o Aprendizado, por outro lado, representa uma oportunidade incrível para os professores oferecerem informações que vão acelerar o caminho para um bom desempenho e transmitir mensagens poderosas de mentalidade aberta para o desenvolvimento do raciocínio. Pesquisas mostram que trocar notas e testes pela Avaliação para o Aprendizado causa um forte impacto sobre o aproveitamento, a autoconfiança, a motivação e as futuras rotas de aprendizagem dos alunos.
Ao usar as avaliações para empoderar os alunos a aprender e crescer, é possível ajudá-los a desenvolver atitudes positivas em relação à matemática e a si mesmos.
 Este artigo contém trechos do novo livro de Jo Boaler, Mathematical Mindsets − Unleashing Students Potential Through Creative Math, Inspiring Messages and Innovative Teaching.
Este artigo contém trechos do novo livro de Jo Boaler, Mathematical Mindsets − Unleashing Students Potential Through Creative Math, Inspiring Messages and Innovative Teaching.
Por que estamos fazendo isso?
Quando o assunto é aprender matemática, vários alunos já sentiram ansiedade/estresse. Muitos receiam que a matemática seja algo em que ou você é bom ou não. Muitos também se sentem pressionados, pois enxergam a disciplina como algo em que ou você está certo ou errado. O que esses alunos têm dificuldade para entender é que a beleza da matemática não está tanto na solução, mas na reflexão e na criatividade envolvidas na tentativa de resolução do problema. Além disso, em geral, eles se sentem pressionados a ter um bom desempenho para obter boas notas e a ansiedade que vivenciam é como uma nuvem carregada que paira sobre suas cabeças. Independentemente do que ocorre em sala de aula ou do quanto eles estão gostando do tópico que estão aprendendo, ainda há a pressão circundante de ter um bom desempenho em troca das melhores notas possíveis. Sejam alunos com alto ou baixo aproveitamento, muitos focam em ter uma boa performance para obter uma determinada nota. Isso tem resultado no foco sobre o desempenho (memorização) em detrimento do aprendizado. Queremos que os alunos gostem de aprender. Sá que não é esse o propósito de ir à escola? Com isso em mente, no ano passado, tentamos fazer uma mudança estimulando os alunos a assumir riscos e a não ter medo de errar. Entretanto, quando chegou o momento de dar notas aos testes, os estudantes ainda foram penalizados por não terem acertado. Como podemos estimulá-los a não ter medo de cometer erros e, então, penalizá-los por errar num teste? As duas mensagens eram conflitantes e nós refletimos sobre o tema durante o curso de férias. Após cuidadosa reflexão, ficamos curiosos para testar isto: O que aconteceria se todo mundo tirasse nota 10 no começo do ano?! Será que a turma já não se sentiria pressionada ou se preocuparia com o desempenho? Será que isso lhes daria mais liberdade para serem criativos e se arriscarem mais? Será que os levaria a ser mais curiosos ou a querer ir mais a fundo para entender por que as coisas funcionam de um determinado jeito? Será que isso os levaria a uma motivação mais intrínseca a querer ter um bom desempenho e aprender? É o que vamos descobrir…
Trecho da carta para os pais, do Departamento de Matemática da escola de Ensino Médio High Tech, em Chula Vista, San Diego.
Referências
Black, P., Harrison, C., Lee, C., Marshall, B., & Wiliam, D. (2002). Working inside the black box: Assessment for learning in the classroom. London: Department of Education & Professional Studies, King’s College.
Black, P. J., & Wiliam, D. (1998a, October). Inside the black box: Raising standards through classroom assessment. Phi Delta Kappan, 139–148.
Black, P. J., & Wiliam, D. (1998b). Assessment and classroom learning. Assessment in Education, 5(1), 7–74.
Boaler, J. (1998). Open and closed mathematics: Student experiences and understandings. Journal for research in mathematics education, 41-62.
Boaler, J. (2015). Mathematical Mindsets: Unleashing Students’ Potential Through Creative Math, Inspiring Messages and Innovative Teaching. San Francisco, CA: Jossey-Bass.
Butler, R. (1987). Task-involving and ego-involving properties of evaluation: Effects of different feedback conditions on motivational perceptions, interest and performance. Journal of Educational Psychology, 79, 474–482.
Butler, R. (1988). Enhancing and undermining intrinsic motivation: The effects of task-involving and ego-involving evaluation on interest and performance. British Journal of Educational Psychology, 58, 1–14.
Deevers, M. (2006). Linking classroom assessment practices with student motivation in mathematics. Paper presented at the American Educational Research Association, San Francisco.
Elawar, M. C., & Corno, L. (1985). A factorial experiment in teachers’ written feedback on student homework: Changing teacher behavior a little rather than a lot. Journal of Educational Psychology, 77(2), 162–173.
Kohn, A. (2011, November). The case against grades. Retrieved from https://www.alfiekohn.org/ article/case-grades/
Lemos, M. S., & Veríssimo, L. (2014). The relationships between intrinsic motivation, extrinsic motivation, and achievement, along elementary school. Procedia – Social and Behavioral Sciences, 112, 930–938.
Pulfrey, C., Buchs, C., & Butera, F. (2011). Why grades engender performance-avoidance goals: The mediating role of autonomous motivation. Journal of Educational Psychology, 103(3), 683–700. Retrieved from https://www.researchgate.net/profile/Fabrizio_Butera/publication/232450947_Why_grades_engender_performanceavoidance_goals_The_mediating_role_of_autonomous_ motivation/links/02bfe50ed4ebfd0670000000.pdf
Stipek, D. J. (1993). Motivation to learn: Integrating theory and practice. New York: Pearson.
White, B. Y., & Frederiksen, J. R. (1998). Inquiry, modeling, and metacognition: Making science accessible to all students. Cognition and Instruction, 16(1), 3–118.